Very sensitive capacitive bridge, measures the delta between C3 and C4, the key is the floating input voltage from the 4 transformers.
R1 is the input impedance of the AD8310 detector.
L9 is there to reduce the drive current.
When C4 = (1+d)*C3, where d<<1 the Thevenin voltage is V1 * d, and the Thevenin impedance (without L9, and without R1) is a reactance of 0.5 * C3
The attainable resolution with such a circuit should be around 10 aF.
A higher resolution is possible, but that would require a higher frequency and noise sensitive air-core transformers.
In this example it is a variation is capacitance which gives an output signal, when C4 is made of isolated electrodes in the plasma, the (very small) dielectric losses and variation in reactance could be used to measure the Debye length.
The capacitor in the plasma (C4) consists of two isolated electrodes, C3 = C4 at vacuum/air, when the space between the electrodes is a plasma with a low Debye length (conducting) C4 will have a higher capacity but low dielectric losses. (output signal high and in phase with input signal), when the Debye length becomes comparable to the distance between the plates, the dielectric losses will be higher and C4 will be close to C3, so that will give a low output signal and a higher phase-shift.
De plasma can be a simple DC discharge.
Since it uses only one stable frequency (10MHz in the example) noise filtering should be simple.




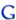






0 reacties:
Een reactie posten